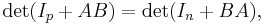Sylvester's determinant theorem
In matrix theory, Sylvester's determinant theorem is a theorem useful for evaluating certain types of determinants. It is named after James Joseph Sylvester.
The theorem states that if A, B are matrices of size p × n and n × p respectively, then
where Ia is the identity matrix of order a.[1]
It is closely related to the Matrix determinant lemma and its generalization.
This theorem is useful in developing a Bayes estimator for multivariate Gaussian distributions.
Sylvester (1857) stated this theorem without proof.
External links
- Related post on the blog of Terence Tao.
References
- ^ David A. Harville. Matrix Algebra From a Statistician's Perspective. Springer, 2008, Pages 416